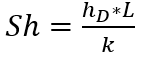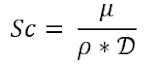Dimensionless Groups in Chemical Engineering

Dimensionless Groups or numbers are relationships with no units of measurement and are often used in chemical engineering.

There are numerous dimensionless numbers used by chemical engineers and this blog entry discusses the more common ones. The equations below are all in metric units, however, if you use consistent units, the dimensionless numbers remain unchanged.

Reynolds Number (Re)

This is arguably the most commonly used dimensionless group in chemical engineering. It gives a measure of the ratio of inertial and viscous forces in fluid flow and is often used to determine if the flow is either laminar or turbulent:

In laminar flow, viscous forces dominate. The flow paths are smooth, streamline and constant.
In turbulent flow, inertial forces dominate. The flow regime is unstable, generating eddies and vortices.

The Reynolds Number can be calculated using the following equation:

Where:

ρ = Fluid density (kg/m³)
u = Fluid velocity (m/s)
L = Characteristic dimension (m)
μ = Dynamic viscosity (Pa.s)

When calculating Reynolds Number, the units used are not important but MUST be consistent. For pipes or channels with circular cross-section, the characteristic dimension can be taken as the pipe diameter.

For flow through pipes, Reynolds Number below 2000 indicates laminar flow while a Reynolds Number above 4000 indicates turbulent flow. Reynold Numbers between 2000 and 4000 indicate transitional flow i.e., rapidly changing between laminar and turbulent flow.

Prandtl Number (Pr)

This is the ratio of kinematic viscosity to the thermal diffusivity. Prandtl Number can also be defined as the ratio of momentum and thermal diffusivities. It tells us how fast the thermal diffusion occurs as compared to momentum diffusion in fluids. It is used in many calculations involving heat transfer in flowing fluids, as it gives a measure of the relative thickness of the thermal and momentum boundary layers. It can be calculated using the following equation:

Where:

C_P = Fluid Specific Heat Capacity (J/kg.K)
μ = Dynamic viscosity (Pa/s)
k = Thermal conductivity (W/m.K)
ν = Momentum or Kinematic diffusivity (m²/s)
α = Thermal diffusivity (m²/s)

It should be noted that the Prandtl number is dependent on the fluid’s physical properties alone and hence it is often found in physical properties.

For many gases (with the notable exception of hydrogen), the Prandtl number has a value of 0.6 to 0.8 over a wide range of conditions. If the Pr << 1, then thermal diffusivity dominates and when Pr >> 1, then momentum diffusivity dominates

Nusselt Number (Nu)

This is the ratio of convective to conductive heat transfer in a fluid over a given length, L:

Where:

h = Heat Transfer Coefficient (W/m².K)
L = Characteristic length (m)
k = Thermal conductivity (W/m.K)

For heat transfer in pipes, the characteristic length is the pipe diameter.

When Nu ≈ 1 then convection and conduction are about equal. Typically, this occurs in laminar conditions. As the Nusselt number becomes larger, convective heat transfer becomes relatively more important – this occurs as the flow becomes more turbulent.

The mass transfer equivalent of the Nusselt number is the Sherwood Number discussed next.

Sherwood Number (Sh)

This is a measure of the ratio of convective and diffusive mass transfer in a fluid. It is analogous to the Nusselt Number in heat transfer and summarized as shown:

Where:

h_D = Mass Transfer Coefficient (m/s)
L = Characteristic length (m)
k = Molecular Diffusivity (m²/s)

Froude Number (Fr)

It is a measure of the ratio of the inertial and gravitational forces and can be expressed as:

Where:

v = Velocity (m/s)
g = Acceleration due to gravity (m/s²)
L = Characteristic length (m)

It is often used to analyze fluid flow problems on a free surface. For example, in agitated vessels, Fr governs the formation of free surface vortices:

Grashof Number (Gr)

This is a ratio of the buoyancy and viscous forces. It is used to calculate heat transfer in natural convection where the fluid velocity depends on buoyancy. It can be expressed as:

Where:

β = Volumetric coefficient of thermal expansion (1/K)
g = Acceleration due to gravity (m/s²)
ΔT = Temperature difference (K)
L = Characteristic length (m)
ρ = Fluid Density (kg/m³)
μ = Dynamic Viscosity (Pa.s)

Mach Number (Ma)

This is the ratio of the fluid velocity to the velocity of sound in that medium. It can be expressed as:

Where:

u = Fluid velocity (m/s)
a = Speed of sound in fluid medium (m/s)

In Chemical Engineering, the Mach Number is commonly used in calculations that involve high velocity gas flow.

Schmidt Number (Sc)

This is the ratio of kinematic viscosity to the diffusivity and it characterizes mass transfer in a flowing fluid. It can be expressed as:

Where:

μ = Dynamic viscosity (Pa/s)
ρ = Fluid Density (kg/m³)
D = Diffusivity (m²/s)

Biot Number (Bi)

It is the ratio of the internal thermal resistance of a solid to the boundary layer species transfer resistance. It can also be defined as the ratio of internal conductive resistance to the external convective resistance. It is represented as shown:

Where:

h = Convective heat transfer coefficient (W/m².K)

L_C = Characteristic Length (m)

k = Thermal conductivity (W/m.K)

Bi < 0.1 indicates the applicability of the lumped heat analysis.

Biot Number helps analyze the interaction between conduction in a solid and convection at its surface. Smaller Bi number values signify that conduction is dominating the heat transfer mechanism while larger Bi number values signify that convection is dominating the heat transfer process.