Introduction to Heat Transfer

Heat Transfer (HT) is the thermal energy in transit due to a temperature difference. This means that the existence of temperature difference leads to HT occurring in a medium or between media.

There are different types or modes of HT processes as listed below:

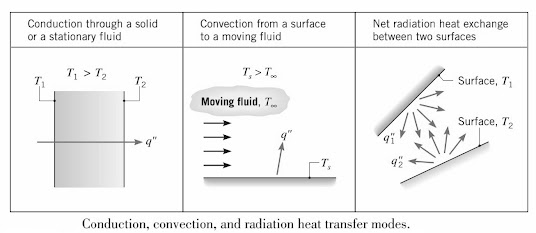
• Conduction – HT that occurs due to the existence of a temperature gradient in a stationary medium, either solid or fluid.
• Convection – HT that occurs between a surface and a moving fluid at different temperatures.
• Thermal Radiation – HT that occurs between two surfaces at different temperatures in the absence of an intervening medium. This is due to the fact that all surfaces of finite temperature emit energy in the form of electromagnetic waves. 

The HT processes can be quantified using rate equations to compute the amount of energy transferred per unit time.

a) Conduction

Can be viewed as the transfer of energy from a more energetic particles in a substance to less energetic ones due to interactions between the particles. Conduction is therefore heat transfer (HT) through a substance that has no bulk (macroscopic) motion e.g., solids.

A high temperature means high molecular energy thus neighboring molecules collide; energy is transferred to the less energetic molecules. Thus, when a temperature gradient exists, energy transfer by conduction occurs in the direction of decreasing temperature.

For heat conduction, the rate equation is known as Fourier’s Law of Heat Conduction.

For a 1 – dimensional plane wall shown above, having a temperature distribution T(x), the rate equation is expressed as follows:

Where:

q_x = heat flux in x-direction

k = thermal conductivity (W/m.K)  [this is a characteristic of the wall material]

dT/dx = temperature gradient

If k is a constant, the heat flux can be calculated as:

The negative sign is due to HT occurring in the direction of decreasing temperature.

Under steady state conditions, the temperature distribution is linear and can be expressed as:

The heat flux can therefore be simplified into:

Or

NOTE: The above equation is the rate of HT per unit area, thus the heat rate by conduction through a plane wall of Area, A, is the product of the heat flux and the area. 

b) Convection

This is heat transfer (HT) between a surface and a moving fluid at different temperatures.

It is comprised of two mechanisms:

• Energy transfer due to random molecular motion (diffusion).
• Energy transfer by the bulk or macroscopic, motion of the fluid. This motion in the presence of a temperature gradient contributes to HT.

Convection is used when referring to the cumulative transport, while advection is the transport due to bulk fluid motion.

A region in the fluid develops where the fluid velocity varies from zero at the surface to a finite value u_∞ at the outer region of the fluid. This region is known as a boundary or hydrodynamic layer.

Also, if the temperature of the surface varies from the flow temperature, the fluid region will have varying temperature from T_s at the surface (y=0) to T_∞ at the outer region of the fluid. This is the thermal boundary layer. If T_s > T_∞ convective HT occurs from the surface to outer flow.

At the surface (y=0), fluid velocity is zero and heat us transferred only by random molecular motion (diffusion) while bulk fluid motion increases as the boundary layer grows.

Convection can be classified according to nature of flow:

• Forced convection - When flow is caused by external means like fans, pumps, wind.
• Free (natural) convection - Flow occurs due to buoyancy forces which are due to density differences caused by the variation in fluid temperature.
• Mixed forced and natural convection.
• Boiling and condensation - For typical convection, energy transferred is the sensible or internal thermal energy, but for these two, there's an addition of latent heat exchange due to phase change.

Below is a table summarizing the heat transfer coefficient of convection processes: 

The general rate equation for convection is known as Newton’s law of cooling and is represented as:

Where:

q_x = convective heat flux (W/m²)

T_s = Surface temperature (K)

T_∞ = Fluid temperature (K)

h = Convection HT coefficient (W/m².K)

c) Radiation

Thermal radiation is the energy emitted by matter at a non-zero temperature. The energy of the radiation is transferred by electromagnetic waves.

While conduction and convection need material medium for heat transfer (HT), radiation can occur efficiently in a vacuum. 

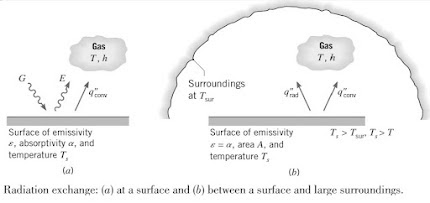
Radiation emitted by the surface originated from the thermal energy of matter bound by the surface as shown below:

The rate at which energy is released per unit area (W/m²) is termed as the surface emittive power, E. For an ideal emitter, this is expressed by the Steffan-Boltzmann law and such a surface is called an ideal radiator or blackbody.

Where:

T = Absolute temperature of the surface (K)

σ = Stefan-Boltzmann constant (σ = 5.67 x 10^-8 W/m⁴.K⁴)

However, for a real surface heat flux emitted is less than that of a blackbody. A radioactive property of the surface known as emissivity, ε. Is used to modify the above equation into the following:

Emissivity is in the range 0≤ ε ≤1 and provides a measure of how efficiently a surface emits energy relative to a blackbody.

Irradiation (G) is the radiation from any source like the sun, that is incident on a unit area of the surface. This radiation can be absorbed, reflected or transmitted by the surface.

Absorptivity (α), is the rate at which radiant energy is absorbed per unit surface area and is in the range 0≤ α ≤1. It can be expressed as:

If α < 1 and surface is opaque, then portions of irradiation are reflected. If surface is semitransparent, portions of irradiation is transmitted.

A special case that occurs frequently involves radiation exchange between a small surface at T_s and a much larger, isothermal surface that completely surrounds the smaller one a T_surr.

When α = ε the surface is called a gray surface.

Irradiation can be approximated by emission from a blackbody at T_surr in which case, G = σT_surr⁴.

For a gray surface, the net rate of radiation HT from the surface per unit area is:

The above equation represents the difference between thermal energy released due to radiation emission and that gained due to radiation absorption.