An
Ideal gas satisfies the following conditions:
- The equation of state is given by; PV = nRT
- Internal Energy is dependent only on temperature.
Enthalpy of an ideal gas is defined as:
This
indicates that enthalpy is also only dependent on temperature.
For a single-phase and single-component system, Gibbs phase rule gives the degrees of freedom as two.
Thus, the state of such system is specified by two independent intensive properties. The dependence of internal energy on temperature and volume leads to a convenient relationship to use in calculating internal energy change. The total differential internal energy is given by:
For
an ideal gas, internal energy is independent of volume, thus the above equation
can be simplified as follows:
The
above two equations are valid for an ideal gas regardless of what kind of
process is considered.
The
dependence of enthalpy on temperature and pressure leads to a convenient
relationship to use in calculating enthalpy change. The total differential of enthalpy
is given by:
For
an ideal gas, enthalpy is independent of pressure, thus the above equation can
be simplified as follows:
The
above two equations are valid for an ideal gas regardless of what kind of
process is considered.
The
relationship between the two heat capacities can be found by differentiation of
the enthalpy of an ideal gas equation with respect to temperature as:










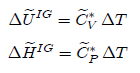

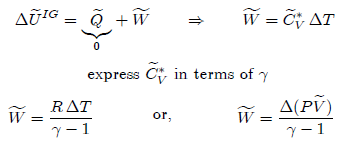









%20Process%20Equations.PNG)
%20Process%20Equations%20-%202.PNG)
%20Process%20Equations%20-%20graph.PNG)
%20Process.PNG)