Constant Volume (Isometric or isochoric) Process
Changes
in internal energy and enthalpy are given by:
For
a constant volume process, the work associated with the displacement of system
boundaries is zero. Besides, if shaft work is zero or negligible, then W = 0. The
amount of transferred heat can be found from the application of the first law
of thermodynamics:
Constant Pressure (Isobaric) Process
The
changes in internal energy and enthalpy are given by:
Furthermore, the heat transferred and work done can be found using the following:
Constant Temperature (Isothermal) Process
Since
temperature remains constant, then:
The work done in a reversible process and heat transferred are found by the following relationships:
Adiabatic Process
An
adiabatic process is one in which the amount of heat transferred between the
system and its surroundings is zero, i.e., Q = 0
The
changes in internal energy and enthalpy are given by:
The work done in a reversible process can be calculated from:
Since
temperature changes in an adiabatic process, evaluation of this integral is
only possible numerically. Thus, it is more convenient to calculate work by the
application of the first law, i.e.,
In
some problems, we may know the values of either pressure or volume at the final
state. Thus, it is necessary to develop equations between T and P, T and V ,
and P and V.
We
can substitute the ideal gas equation of state below into the above equation to
eliminate volumes terms and get a relationship between P and T. The same can
also be done to eliminate T and get an relationship between P and V.
Polytropic Process
The
relationship between pressure and volume during compression and expansion of
gases is sometimes expressed as:
where
n is a constant for any given change. Such processes are called polytropic
and the equations available for adiabatic processes can also be used for
polytropic ones by replacing γ with n.






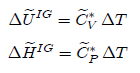

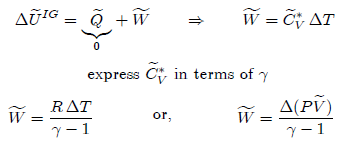







No comments:
Post a Comment