We know that for a variety of processes, the entropy of the universe increases for an irreversible process and remains constant for a reversible process:
If we assume the universe to be an isolated system, we
can rephrase the Second Law as
“Any spontaneous process occurring in an isolated
system will always result in an increase in that system’s entropy.”
Thus:
- For an isolated system, if an entropy increase is not possible, then a spontaneous change cannot occur in that system. This is possible if the entropy of an isolated system is at its maximum value. The condition of maximum entropy i.e., no possible spontaneous change is called the state of thermodynamic equilibrium.
- The statement: “the entropy of a system can never decrease” only applies to an isolated system. Generally, the entropy of an arbitrary system can be decreased by a suitable heat interaction.
- In order to determine the priority of a process occurring in the universe, we have to apply the principle of entropy increase. That is, any spontaneous process following a previous process must have a higher entropy than the preceding process. Thus, entropy is referred to as time’s arrow.
It should be noted that there is no such thing as the
conservation of entropy. Real processes always generate entropy and, as a
result, entropy of the universe always increases.
a) Entropy and the Loss of Work
Let us consider a rigid, well-insulated tank divided
into two equal volumes A and B by a membrane. Side A is filled with 1 mol of an
ideal gas at 300K and 1bar and the side B is evacuated. If the membrane
ruptures so that the gas fills the entire volume, what would be the entropy change?
System: The contents of the tank.
Using the 1st law of thermodynamics:
Since the internal energy of an ideal gas is dependent only on temperature, the final temperature is also 300K. We can use the following equation to help calculate the entropy change of the system:
Thus, the entropy change of the system can be solved by simplifying the above equation. Also, since there is no heat interaction between the system and its surroundings, entropy change of the surroundings is zero. Thus:
To compare this irreversible process with a reversible
one between the same initial and final states, we can consider 1 mol of an
ideal gas at 300K and 1 bar in a piston-cylinder assembly. If we assume that
the gas expands until the volume doubles against a frictionless piston while
heat is reversibly transferred to the gas in order to keep the gas at a
constant 300K. Thus the entropy change of the system is:
The amount of heat transferred to the gas can be
calculated using equation 7:
When the gas expands irreversibly in a rigid and
well-insulated tank, we see that the entropy of the system increases
and no work is done by the system. Conversely, reversible
expansion of the gas from the same initial state to the same final state increases
the entropy of the system by the same amount but, in this case, work is
done by the system.
In the reversible process, the increase in the entropy
of the system is compensated by the decrease in the entropy of the surroundings
so that ΔSuniverse = 0. In other words, entropy is transferred from
the surroundings into the system. Thus, entropy generation corresponds to the
decrease in the ability of energy to do work.
If energy is a measure of system’s ability to do work,
entropy is a measure of how much this ability has been devalued. Entropy
generation is directly related to the lost work.
b) Entropy and Probability
One mole of a gas contains N molecules, where N is the
Avogadro’s number (N = 6.02 × 1023).
Let us consider a rigid, well-insulated tank divided
into two equal volumes by a diaphragm with a hole in it and the tank contains 1
mol of an ideal gas.
Note that the probability of finding all the molecules
in the tank is unity.
Hypothetically, if we capture one of the molecules and
paint it red, the probability of finding that red molecule on the left side is 1/2.
If we capture another molecule and paint it white, the probability of finding
both the red and white molecules on the left side is (1/2)(1/2) = (1/2)2.
The probability of finding all the molecules on the left side is almost zero
and equal to (1/2)N.
It doesn’t matter where the position of the diaphragm
is, the probability of finding all the molecules on the left side is (V1/V2)N,
where V1 is the volume to the left of the diaphragm and V2
is the total tank volume.
If we suppose that the gas is initially contained on
the left side. By puncturing the diaphragm, the gas fills the entire tank. In
this way, the gas goes from a state of low probability to a state of high
probability. Let P1 and P2 represent the initial and
final probabilities, respectively. Thus,
During expansion, the internal energy and the
temperature of the gas remains constant.
As a result, the right-side of Equation 14, gives the
change in entropy of an ideal gas during isothermal expansion from V1
to V2. Therefore, Equation 14 becomes:
Thus, the increase in entropy during a spontaneous process
corresponds to the transition from a state of lower probability to a higher
probability.
c) Entropy and Disorder
In a system the entropy increases with increasing
disorder. Thus, the disorder in the universe is always increasing.
As the system changes to a more orderly state, its
entropy decreases. Some examples are:
- During phase transformation, i.e., Liquid to solid and gas to liquid
- As the temperature of a substance decreases
- As the pressure of a gas increases.
The molecules of a perfect crystal at 0 K have no internal energy, hence the molecules are perfectly ordered in the crystal lattice.
Thus, one can assign the value of zero to the entropy for this
idealized state of maximum possible order. This assignment turns out to be very
useful and is sometimes referred to as the third law of thermodynamics.





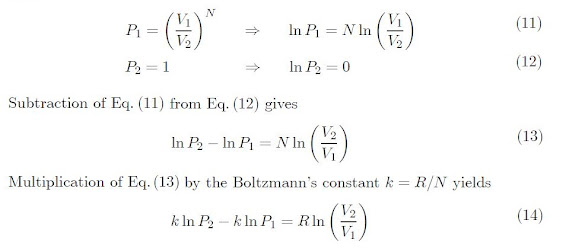
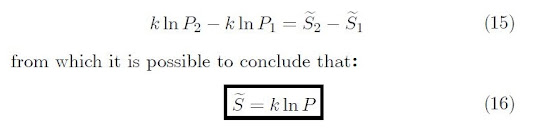













.JPG)
.JPG)

.JPG)