Reactor sizing was discussed in a previous blog entry (Click here to view).
Example 1
Consider a liquid phase reaction occurring in a PFR with the following data and Equation
|
X |
0 |
0.4 |
0.8 |
|
-rA
(mol/dm3s) |
0.01 |
0.008 |
0.002 |
|
1/(-rA)
(dm3s/mol) |
100 |
125 |
500 |
If the molar feed to the PFR is 2 mol/s, what is the volume of the PFR needed to achieve 80% conversion.
Answer
For a PFR,
Using the data provided in the table, we can plot a Levenspiel Plot:
Using Simpson's three point rule:
Thus, to achieve an 80% conversion, a PFR of 293.3 dm3 is needed
Example 2
A second order
irreversible reaction is carried out in the gas phase inside a PFR.
A reactant of molecular
weight 40 and 50% by weight, and the rest with an inert of molecular weight of
20 are fed to the reactor. The reaction is carried out at constant temperature
of 70°C and constant pressure of 5.25 atm. The rate constant is 400m3/(kmol.ks).
Calculate the volume of
the PFR needed to achieve a 40% conversion of A to produce 30kmol/hr of product
R.
Answer
For a second order reaction:
When substituting into the PFR equation and integrating the equation we get:
To calculate εA, let us consider a 1.0g sample of reagent mixture which has 0.5/40 = 0.0125 mol of A and 0.5/20 = 0.025 mol of inert. The following volume balance is then obtained.
The expansion parameter, εA, = (0.05 - 0.0373)/0.0373 = 0.0340
The initial concentration of A, CA0, is given by:
Substituting into equation 1,
Given the product flow
rate (FR) is 30 kmol/hr, we can obtain the volumetric flow rate:
The reactor volume can now be found using the following:




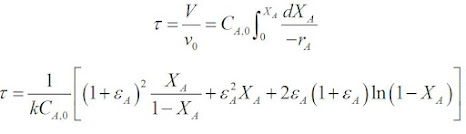

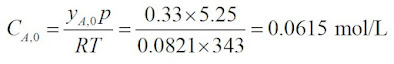







No comments:
Post a Comment