Example 1
The following reaction is irreversible and first order:
The reaction is carried out in a PFR with 80 tubes. Each tube has a diameter of 5cm and a height of 1m. The feed consists of reactant A and 30% inerts flowing at 200kg/h with a pressure of 50bar and temperature of 600°C (873K). The output conversion is 90%. What is the average residence time? (The molecular weight of A is 60g/mol & R = 0.0821 L • atm/ mol • K)Solution
The space time for a first order
reaction in a PFR is given by the following equation:
The mass flow in each tube is: (200/80) = 1.25kg/h
In molar basis:
Thus, the initial concentration of A is given by:
We can now calculate the initial
volumetric flow:
The volume of each tube can be calculated as follows:
The residence time can be
calculated as follows:
The expansion
parameter, εA can be determined as follows:
The rate constant, k,
can now be solved using equation 1:
Example 2
The following second order irreversible reaction is carried out in gas phase in a PFR reactor:
The PFR feed consists of 50%
by weight reactant A (MW = 40) and the rest is inert (MWinert = 20).
The reaction occurs at a constant temperature of 70C and pressure of 5.25atm.
The rate constant is 400m3/(kmol.ks).
For a production rate of R set at 30kmol/h with a 40% conversion, what should be the volume of the
reactor?
Solution
For a second-order reaction, the rate can be expressed as:
Substituting the PFR design equation into the above equation and integrating we obtain:
With a mass basis of 1.0g, we can calculate εA. The molar values for each feed components are 0.5/40 = 0.0125 mol of A and 0.5/20 = 0.025 mol of inert. Thus, the volume balance is as shown below:
The expansion parameter, εA is = (0.05 - 0.0373)/0.0373 = 0.340. The initial concentration of A is:Equation 1 can now be solved:
Given that the output molar flow FR = 30kmol/h, the volumetric flow rate, vo is:
Thus, the reactor volume is:











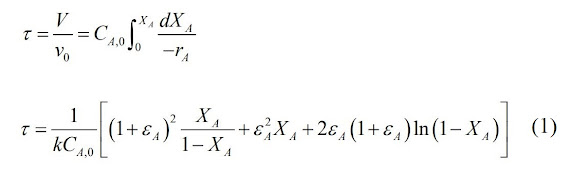









No comments:
Post a Comment