Introduction to Mass Transfer

Mass transfer is the movement of particles or molecules from one point to another under the influence or a concentration gradient i.e., from an area of high concentration to an area of low concentration. This movement of particles occurs due to two mechanisms: Molecular diffusion and mass convention.

Molecular Diffusion

This refers to the movement of individual molecules through a group of molecules without the aid of a bulk fluid flow like stirring. Imagine a few molecules of a liquid A placed in a particular location within a larger group of molecules of liquid B. As the molecules undergo movement through Brownian Motion, the molecules of A will eventually be distributed into various locations within liquid B as shown below:

The rate of transfer of molecules of A through molecules of B from one location to another is through molecular diffusion. This is mathematically described using Fick's Law. This is simplified into rate of transfer of species A by molecular diffusion in the x-direction as shown in the molecular diffusion equation below:

 

Where:

Ṅ_A,x = diffusion transfer rate of species A (moles transferred per unit time e.g., gmol/s) across area A in the x direction between locations 1 and 2.

A = cross sectional area across which the diffusion occurs (perpendicular to the x direction)

D_AB = the binary diffusivity coefficient of species A in species B with units of area per time (e.g., m²/s)

c_A = concentration of species A (e.g., gmol/mol)

 

The figure below shows the molecular diffusion of a molecule in the x direction through a cross sectional area, A.

 

The transfer rate can be simplified in terms of a driving force (Δc_A), which tends to produce the diffusion, and a resistance (Δx/D_ABA), which tends to oppose the diffusion. The binary diffusivity, D_AB, describes the ease with which a molecule of species A moves through the molecules of species B. Thus, when D_AB is large and transfer occurs rapidly, the resistance is small and when D_AB is small and transfer occurs slowly, the resistance is large. D_AB is not a constant and it varies with the physical conditions like temperature of the system. The temperature affects the motion of the molecules. Thus, the factors affecting D_AB depend on the properties of the molecules of A and B and are listed below:

• molecular size – this determines the distances and spaces between the molecules
• molecular shape – includes the presence of long chains that can tangle
• molecular charge – affects the attractive or repulsive forces between the molecules.

 

Mass Convection

This is the method by which velocities and flow help the molecules of different types mix. In the figure below we can see a small current of fluid moving in the direction represented by the dark arrow which carries the molecules in its path to the new locations. Even though the molecules undergo molecular diffusion, the convection dominates as a transfer mechanism.

Mass convection distributes molecules faster than molecular diffusion alone.

A frequent application of mass transfer in chemical engineering processes is the transfer of materials across a phase boundary (interface) where two phases (solid, liquid and/or gas) meet. In the design of process that have mass transfer across phase boundaries, chemical engineers include mass convection flow to increase that transfer. In mass transfer by convection at phase boundaries, the net effect is the transport perpendicular to the phase boundary as shown below, where the net transfer direction is indicated by the large arrow. In this figure, the transfer mode of species A in Phase I is not specified in order to focus on Phase II.

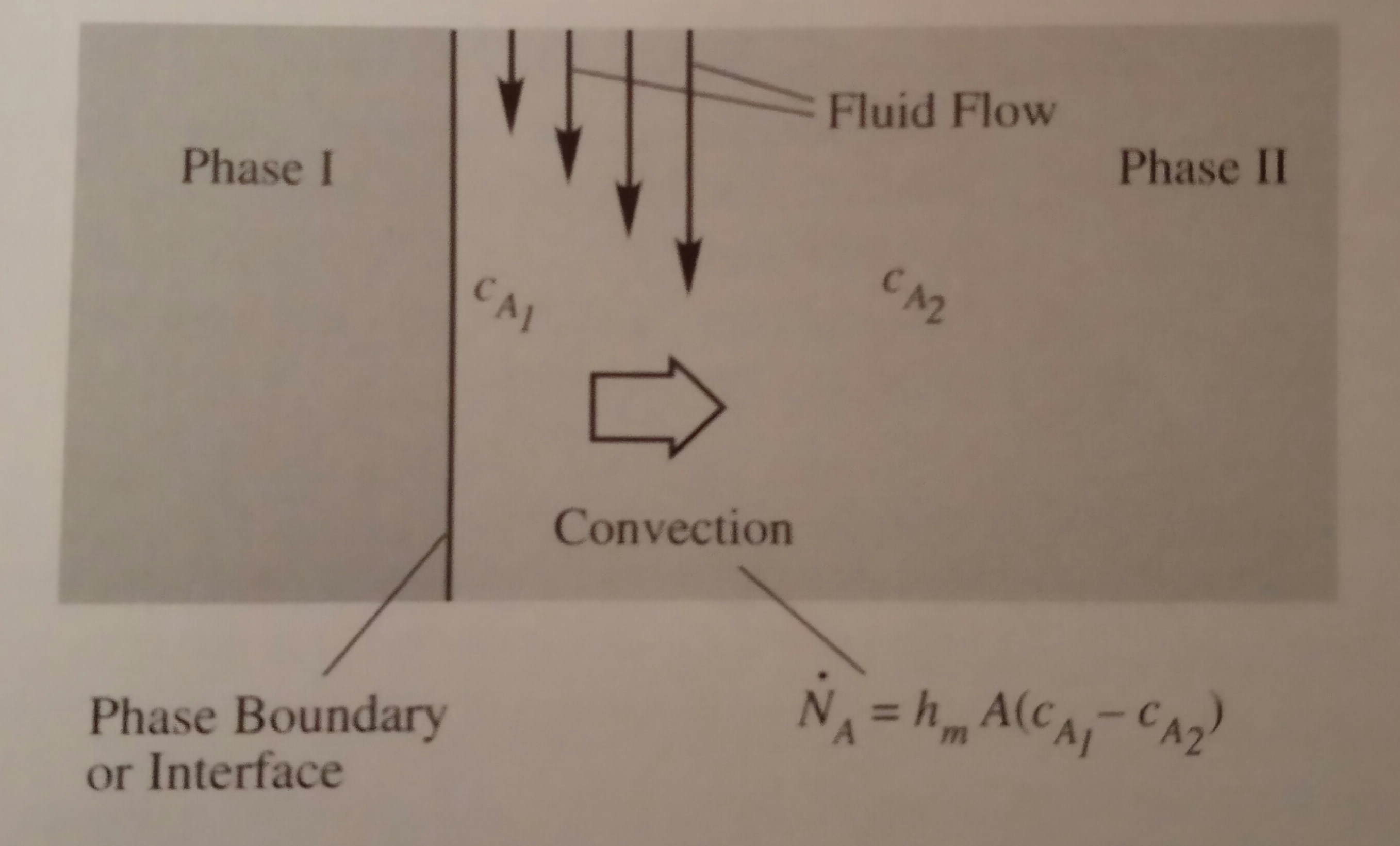
The following equation for mass convection quantitatively describes the transport to/from phase boundaries via convection:

where:

c_A1 = concentration of species A at the starting location (1) of transfer (at the phase boundary)

c_A2 = concentration of species A at the ending location (2) of transfer (at the bulk of fluid)

Ṅ_A = convection transfer rate of species A through area A from locations 1 to 2

h_m = mass transfer coefficient, which accounts for the effects of diffusion and fluid motion (unit length per time)

A = cross sectional area through which the transfer occurs

In the equation of mass convection shown above, the driving force is present in the concentration difference just as in the molecular diffusion equation. For mass convection, the resistance is 1/h_mA. Thus, if h_m is large, the resistance is small and transfer occurs rapidly and when h_m is small, the resistance is large and transfer occurs slowly.

 

 

 

 

Reactor Space Time and Space Velocity

Another important factor in reactor design is space time and velocity. These are discussed below:

Where:
Liquid-hourly space velocity (LHSV)
Gas-hourly space velocity (GHSV)

Design Equations for Continuous Flow Reactors

The previous post dealt with the design equations for a batch reactor, this post will look at the most common reactor types, Continuous Flow Reactors like CSTR and PFR:

Design Equations for a Batch Reactor

Reactors need to be optimally designed in order to have an efficient and safe process. For Chemical Engineers it is important to learn design equations for the different types of reactors available. Below are the design equations for a Batch Reactor:

Temperature and Heat

TEMPERATURE AND HEAT

TEMPERATURE

There are numerous measurable physical properties that vary as temperature varies. these can be:

·       Liquid volume

·       The length of a rod

·       A wire’s electrical resistance

·       The pressure of a gas kept at constant volume

·       The volume of a gas kept at constant pressure.

 

Isothermal Process

This is a process that occurs at a constant temperature. It is important to note that if the initial and final states are at the same temperature, it does not necessarily imply that it’s an isothermal process.

Exercise: Which of the following processes are isothermal?

a)     A tank of compressed air at room temperature leaks air through a tiny leak.

b)     A large valve in the tank above is opened allowing the pressure to fall to atmospheric pressure.

c)     Heat is added to water boiling on a stove.

d)     The pressure of air in a piston-cylinder device is quickly increased from 1 bar to 15 bar.

 

Solution: Processes (a) and (c) are isothermal. In process (a), the rate of gas escape is so slow that time is ample for heat transfer to keep the temperature constant. Processes (b) and (d) are not isothermal because they are too rapid for the significant heat transfer required to keep the temperature constant.

HEAT

Heat is the transfer of thermal energy from one system to another due to a temperature difference between the two i.e., heat flows flow a higher to lower temperature. For any given substance the amount of thermal energy is measured by temperature. Temperature is a measure of the average kinetic energy of individual molecules. Thermal (or internal) energy, refers to the total energy of all the molecules in the object. The higher the temperature, the more thermal energy is present. However, an increase in thermal energy need not raise the temperature if there is a change of phase, as in the boiling water.

According to the sign convention for heat, if the system receives heat from the surroundings, it is positive. Otherwise, it is negative.

Heat Capacity

The amount of heat, Q, required to change the temperature of the system is found to be proportional to the mass, m, of the system and to the temperature change, ΔT. This implies

where the proportionality constant K is defined as:

Therefore, Q can be defined as follows:

Ĉ_v (or, Ĉ_p) can be viewed as the energy required to raise the temperature of the unit mass of a substance by one degree as the volume (or, pressure) is maintained constant. A common unit for heat capacity is kJ/kg.K or kJ/kg.°C. For solids and liquids Ĉ_v ≈ Ĉ_p.

For gases, however, Ĉ_p is always greater than Ĉ_v because at constant pressure the system is allowed to expand and the energy for this expansion work must also be supplied to the system. For monatomic and diatomic gases, Ĉ_v and Ĉ_p values are given as:

The above relationships can be expressed in the following way for an ideal gas:

Heat capacities of gases are only moderate functions of temperatures and thus for ordinary changes in temperature, i.e., up to several hundreds of degrees for air, the use of constant heat capacities is valid for engineering purposes. If heat capacities are dependent on temperature, then they are expressed as follows:

Specific Heat

This is the ratio of the amount of heat necessary to cause unit change in temperature of a unit mass of the material in question to the amount of heat necessary to raise an equal mass of water one unit on the temperature scale, both processes being carried out along paths subject to the same restrictions, i.e., either at constant pressure or constant volume.

Note that specific heats are dimensionless quantities, whereas heat capacities have the dimensions of energy/(mass) (degree of temperature).

 

Adiabatic Process

This is a process that has no heat transfer between the system and its surroundings. There are two ways a process can be adiabatic:

·       A well-insulated system so that only negligible heat can pass through the boundary.

·       Both the system and its surroundings are at the same temperature, thus no driving force i.e., temperature difference, for heat transfer.

An adiabatic process should not be confused with an isothermal process. Although there is no heat transfer during an adiabatic process, the temperature of a system can be changed by other means such as work.

In determining whether a given process is adiabatic or isothermal, note the following characteristics of these two processes:

·       Heat transfer is a slow process and hence usually negligible in processes that take place very rapidly. There is no way to be absolute in this statement because slow and rapid are relative terms. Nevertheless, processes that occur in a matter of seconds can usually be assumed to be adiabatic.

·       Processes that occur slowly allow time for heat transfer and are usually assumed to be isothermal. The adiabatic and isothermal processes are often opposite extremes. In reality, processes fall in between.