Isolated System
In
an isolated system neither mass nor energy is exchanges with the surroundings.
Thus,
dmin
= 0
dmout
= 0
dQ
= 0
dWs
= 0
Thus,
the general energy equation simplifies as follows:
This indicates that in an isolated system, energy is converted from one form to another but the total energy remains constant. Note that this is the statement of the first law of thermodynamics.
Closed System
For
a closed system, mass cannot cross the boundary. Hence,
dmin
= dmout = 0
Thus,
the general energy equation simplifies as follows:
where
the term dW includes the work associated with the displacement of the system
boundaries, i.e., expansion or contraction, and shaft work. Integration of the
above equation results in:
ΔU
+ ΔEK + ΔEP = Q + W
In
most practical applications, both ΔEK and ΔEP are
negligible. Thus, the equation simplifies as follows:
ΔU
= Q + W
Steady-State Flow System
Under
steady-state conditions, dmsys/dt = 0, indicating that the total
mass of the system does not change with respect to time.
dmin
= dmout = dm
Since
the boundaries of the system are fixed, dVsys = 0. Under these conditions, the
general energy equation reduces to;
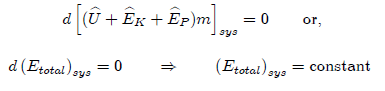
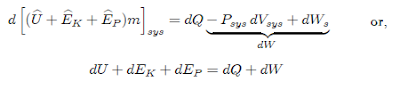
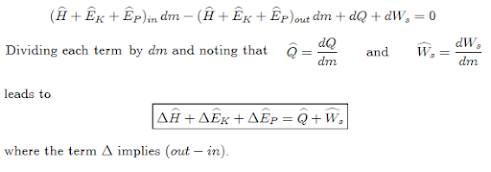




No comments:
Post a Comment