Inventory Rate Equation
Chemical
species, mass, momentum, and energy are concepts that form the basis of science
and engineering and are all conserved quantities.
For
any conserved quantity, φ, an inventory rate
equation can be written to describe its transformation. Inventory of
the conserved quantity is based on a specified unit of time, which is reflected
as a rate and it takes the form:
Unsteady State Mass Balance
For
a single component system, if ρ is the mass density and v is the
velocity vector, then the mass flux (mass per unit time per unit area) is given
by:
Unsteady State Energy Balance
The
conservation statement for total energy under unsteady-state conditions is
given by:
[Rate
of energy in] - [Rate of energy out] = [Rate of energy accumulation]
The
rate of energy entering or leaving the system by a flowing stream is given by:
Flow Work
To
proceed one step further, it is necessary to introduce the concept of flow
work. This is a type of work in a flow system.
Consider
a fluid of mass (dm) flowing into an open system through a circular duct of
cross-sectional area A. As this differential mass crosses the boundary of the
system, the resisting pressure P may be assumed to remain constant since the
differential volume of the mass (dm) is very small compared to the volume of
the system.
The
work done on the system to push the fluid of mass (dm) against a constant force
F = P A is given by:
dW
= P A dx = P dV
This
is the flow work. Note that the flow work is positive when fluid enters the system,
and negative when fluid leaves the system.
Development of the General Energy Equation
The
rate of work done on the system by the surroundings and it is composed of the three
terms:
Where:
A
= Work associated with the expansion or compression of the system boundaries
B
= Shaft Work
C
= Flow Work
Substituting
the above equation into the equation for rate of energy entering or leaving the
system by a flowing stream and using the definition of enthalpy results in the general
energy equation which is expressed below:
In
most practical applications, changes in kinetic and potential energies are
negligible thus the above equation can simplify as:
The
term dW in above equations includes the work associated with the displacement
of system boundaries and the shaft work.



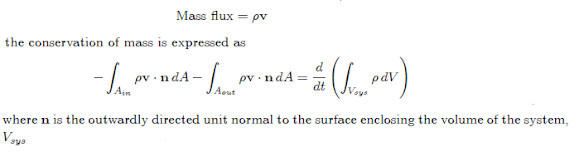











No comments:
Post a Comment