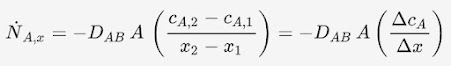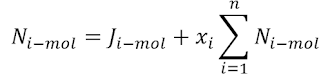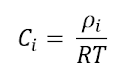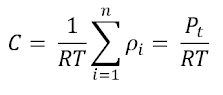Carnot Cycle

How can you convert heat into mechanical energy and work?

• One can use a steady-state flow device like a turbine where the thermal energy of a flowing fluid can be converted to mechanical energy.
• Another technique is the use of a thermodynamic cycle. In this process, a working fluid like air or steam undergoes a series of state changes and finally returns to its initial state. 

The Carnot cycle is the most efficient thermodynamic cycle where an ideal gas in a frictionless piston-cylinder device undergoes the following 4 reversible successive processes:

1. The ideal gas undergoes an isothermal and reversible expansion through the addition of heat from a hot reservoir at a temperature, T_H,
2. The adiabatic and reversible expansion of the ideal gas,
3. The ideal gas undergoes an isothermal and reversible compression by discarding heat to a cold reservoir at a temperature, T_C,
4. And finally, the adiabatic and reversible compression of the ideal gas to its initial state.

This can be schematically represented as follows:

This process can also be graphed onto a P-V graph as shown below:

If we consider our system as an ideal gas in a frictionless piston-cylinder assembly, the analysis of the Carnot cycle is as follows:

Process 1 to 2 (Reversible isothermal expansion at T_H)

Let us take the 1^st law of thermodynamics for a closed system and work done by an ideal gas:

Process 2 to 3 (Reversible Adiabatic Expansion)

Once again let us take the 1^st law of thermodynamics for a closed system and work done by the ideal gas:

Process 3 to 4 (Reversible Isothermal Compression)

Once again let us take the 1^st law of thermodynamics for a closed system and work done by the ideal gas:

Process 4 to 1 (Reversible Adiabatic Compression)

Once again let us take the 1^st law of thermodynamics for a closed system and work done by the ideal gas:

Thus, if we look at the net work output of the Carnot cycle,

If we apply the first law of thermodynamics to the Carnot cycle:

The Efficiency of Carnot Cycle, η

The efficiency, η, can be derived as follows:

Since the processes 2 to 3 and 4 to 1 are reversible and adiabatic, equation 17 can be further simplified as follows:

If we combines Equations 19 and 20 we get the following equation 21:

 (21)   

The Carnot cycle is the most efficient heat engine operating between two constant heat reservoirs T_H and T_C. A heat engine is any mechanism that operates cyclically with the primary purpose to partially convert heat into work. 

Note that: W_net = Q_H - Q_C                        (22)

Using this new notation, Equations 16 and 19 combine as follows:

Substituting Equation 22 into 23 we get:

Finally, with all these new notations, we can represent the Carnot Cycle in a simpler way as shown:

Solved Examples

Example 1

A Carnot cycle receives 1000 kJ of heat at 800°C and rejects heat at 300°C. Calculate the work output.

Solution

From Equation 23:

Substituting the provided values into the above equation:

Thus:

W_net = 466 kJ

Example 2

Suppose an iceberg weighing 10¹⁰ kg drifts into the Gulf stream which has a temperature of 22°C. If we operate a Carnot heat engine using the Gulf stream as a heat source and the iceberg as a cold sink, what is the work output that could be generated while the iceberg is melting?

Solution

Assume that the temperature of the iceberg is 0°C and the heat of fusion for ice is 334,880 J/kg. Take the iceberg as the heat sink.

The amount of heat rejected to the sink is:

Q_C = (10¹⁰) (334,880) = 3.35 × 10¹⁵ J

The amount of heat absorbed can be calculated using equation 24:

 

 

Diffusion in Mass Transfer

 Mass Transfer is the net movement due to a concentration gradient of a component in a mixture from one location to another. Generally, this transfer occurs between two phases across an interface. Mass transfer can also be defined as the selective permeation through a non-porous polymeric material of a component of a gas mixture.

Mass transfer models can be used to describe processes like the passage of a species through a gas to the outer surface of a porous adsorbent particle and into the pores of the adsorbent, where the species is adsorbed on the porous surface.

Mass transfer occurs through two basic mechanisms:

(a) Molecular diffusion by random and spontaneous microscopic movement of individual molecules in a gas, liquid, or solid due to thermal motion

(b) Eddy (turbulent) diffusion by random macroscopic fluid motion.

Molecular Diffusion vs. Eddy Diffusion

Both diffusion types involve different species moving in opposite directions. When a net flow occurs in one of these directions, the total rate of mass transfer of the individual species is increased or decreased by this bulk flow or convection effect, which is a third mechanism of mass transfer.

Molecular diffusion is extremely slow, while eddy diffusion, when it occurs, is orders of magnitude more rapid.

Molecular diffusion typically occurs in solids and fluid involving stagnant, laminar or turbulent flow while eddy diffusion occurs in fluids with turbulent flow.

• In a binary mixture, molecular diffusion occurs due to one or more driving forces like:
• differences in concentration (ordinary diffusion)
• pressure (pressure diffusion). This requires a large pressure gradient which is achieved for gas mixtures with a centrifuge.
• temperature (thermal diffusion). Temperature gradients can be achieved by using thermal diffusion columns to separate liquid and gas mixtures
• external force fields (forced diffusion) that act unequally on the different chemical species present. This is achieved by using an electric field to cause ions of different charges to move in different directions at different speeds

When both molecular diffusion and eddy diffusion occur, they take place in parallel and are additive. Furthermore, they take place because of the same concentration gradient. 

Describing diffusion quantitatively

Assume that molecule A is diffusing between boundary 1 and 2 with fixed concentrations c_A,1 and c_A,2 respectively. The rate of diffusional mass transfer (moles/time) across an area, A, can be determined. A represents an area of y by z in the following illustration:

Fick’s Law of Diffusion

The concentration profile is linear for any system with only pure diffusion (no convection, no reactions, constant properties). Thus, Fick’s law can be approximated as:

The driving gradient for diffusional mass transfer is the difference in concentrations i.e., c_A,1 - c_A,2

Variable	Definition	Units
ṄA,x	moles of species A transferred per unit time from location 1 to location 2	mol/s
DAB	the diffusion coefficient of species A through medium B	m2/s
A	the area through which transfer occurs	m2
cA,1 - cA,2	the concentration gradient between locations 2 and 1	mol/m3
x2-x1	The distance between locations 2 and 1	m

NOTE: the area for mass transfer is not the ‘edge-view’ area but the ‘face-view’ area. This is the area used in Fick’s Law and Fourier’s Law calculations:

In some cases, mass transport occurs through a porous membrane with a pore fraction of ε_pore. In such cases, the actual area available for mass transfer is only the porous fraction of the total, and thus,

A = A_apparent ε_pore

Diffusion Coefficient

The diffusion coefficient, D_AB, is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species.

Theoretically, the diffusion coefficient is proportional to the mean squared displacement divided by the time elapsed: 

The value of the diffusion coefficient is determined through experiments, theory and estimation

The properties that influence the diffusion coefficient of molecule A in solution B are:

• molecular weight of A and/or B,
• molecular size of A and/or B,
• molecular properties like charge, ionic strength, dipole moment of A and/or B,
• temperature,
• pressure.

Equimolecular counter diffusion

This occurs when the mass transfer rates of the two components are equal and opposite.

It occurs in the case of the box with a movable partition and also in a distillation column when the molar latent heats of the two components are the same (λA = λB).

 

Definition of Flux Terms in Mass Transfer

Flux is defined as the amount of a quantity that is transported per unit time across a unit area that is perpendicular to the direction of transport. The molar flux of species i with units’ moles/m².s is represented as:

Where:

N_i-mol is the molar of species i

u_i is the velocity of i with respect to a fixed reference frame.

 

Similarly, the mass flux, N_i-mass, with units mass/m².s is represented as:

In some cases, it is convenient to interpret the total flux of species i with respect to an arbitrary reference frame rather than a fixed set of reference frame.

The molar flux of species i based on an arbitrary reference velocity u₀ is denoted by J_i-mol and is defined as:

Similarly mass flux of species i based on arbitrary reference velocity u₀ is denoted by J_i-mass which can be expressed as:

In a system a frame of moving reference must be chosen, since several molecular species move with different average velocities. The important moving references are mass average, molar average and volume average velocities.

Mass average velocity

This can be defined in terms of the mass concentration and the velocity of species i based on a fixed axis. It is expressed as:

Molar average velocity

This can be expressed by the expression analogous to the mass average velocity. It can be represented by replacing the mass concentration of species i, ρ_i with the molar concentration of species i, C_i:

Volume average velocity

This is important for experimental analysis in a fixed system of constant volume. The volume average velocity can be expressed by:

where v_i is the partial molar volume of species i.

Relation Between Fluxes

The molar flux of species i described previously can be obtained with respect to the molar average velocity as follows:

Substituting the molar flux of species i into the above equation and rearranging it results in:

Substituting the definition of molar average velocity into the above equation we get:

or:

Definition of Concentration Terms in Mass Transfer

For a particular species, its concentration can be expressed in several ways.

In mass transfer applications, the only driving force is the concentration gradient while other driving forces like temperature and pressure gradients are kept constant. There needs to be a gradient of chemical potential between two points to create a driving force that allows mass transfer to occur.

A concentration gradient is a spatial difference in the abundance of the chemical species.

A concentration profile is a sketch indicating the magnitude of the concentration as a function of position and is often superimposed on a process to indicate where these changes occur. It is analogous to the velocity profile in fluid flow examples and illustrated below:

Mass concentration or molar concentration of components and mass or mole fraction of species are used to express concentration gradients.

Mass Concentration

For any species i, the mass concentration is expressed as ρ_i. It is defined as the mass of i per unit volume of a multi-component mixture. This is expressed as follows and has the same units as density:

Total mass concentration within a mixture is equal to overall density which can be expressed as follows, where n is the number of species in a mixture:

Mass Fraction

The mass fraction of species i (w_i) is the ratio of mass concentration of species i to the total mass density and can be expressed as:

From the definitions used for mass concentration into the above equation, we obtain the following expression:

Molar Concentration

The molar concentration (C_i) of component is the number of moles of the i^th component per unit volume of mixture. The total concentration in the system can be obtained by adding up all the molar concentrations of all the species in the mixture and is represented as:

To convert from mass to molar concentration, divide the mass concentration of species i by its molar weight. For an ideal gas mixture, the molar concentration of species i can be obtained from the ideal gas law (PV = nRT) as follows:

Where:

• ρ_i is the partial pressure of species i in the mixture,
• T is the absolute temperature,
• R is the universal gas constant. 

Thus, the total concentration in the gaseous system can be represented by:

Mole Fraction

The mole fraction of species i in a mixture is found by dividing the molar concentration of species i by total concentration in the system and is expressed as;

and

The summation of mole fractions of species in a mixture always adds up to 1 as shown:

Introduction to Mass Transfer II

 As previously defined (Click here) Mass transfer is the movement of components under a chemical potential gradient from an area of high concentration to that of a lower concentration. Once the gradient equals zero then equilibrium is established.

Mass transfer depends on the diffusion of molecules from one distinct phase to another. It is based on the differences in physical and/or chemical properties of the molecules in motion. These properties include solubility and vapor pressure. For interphase mass transfer, a concentration gradient exists between the bulk and interface. Under steady state conditions an interface equilibrium is assumed. An interface is the boundary between different phases.

Many industrial processes depend on mass transfer which aids in the movement of materials from one homogeneous phase to another. These include:

Adsorption and desorption – This process uses the ability of molecules to move from either gas or liquid phase to the surface of solid particles. Adsorption does not qualify as a true inter phase mass transfer operation as the fluid adheres to the solid surface instead of dissolving in the solid. Desorption is the opposite of adsorption as mass transfer occurs from the solid surface (adsorbent) to the liquid or gas phase (adsorbates).

This process is applied in:

• Removing toxic gases and smells from the air.
• Solvent recovery
• Removing ions from solutions

Adsorption is also discussed here.

Absorption and stripping – Absorption is the transfer of materials from a gas to a liquid phase. The gas is absorbed by a liquid in which the solute gas is more or less soluble from its mixture with an inert gas, as well as more or less insoluble gas. The liquid is immiscible in the gas phase. An example of absorption is the separation of ammonia from an air-ammonia mixture using water with the solute recovered from the solution using distillation. Absorption is also discussed here.

Stripping is the separation of a gas solute from a liquid phase.

Distillation – This is a process where a miscible, volatile liquid mixture is separated into its individual components using partial vaporization. The components vaporize when their boiling points are reached then are condensed into their liquid states. This is widely used in the purification of crude oil into gasoline, kerosene, fuel oil and lubricating oil.

In industrial applications, distillation commonly occurs in a distillation column. Some majore aspects of a distillation column are discussed here.

Extraction – This is a process where the separation of the constituents of a liquid solution is achieved by contact with another insoluble liquid. The liquid used to achieve this process is called a solvent while the solution to be extracted is called a feed. The product which is solvent rich is referred to as the extract while the residual liquid from which the solute is removed is called the raffinate.

Real world applications include the separation of aromatics from kerosene-based fuel oils, the production of fuels in the nuclear industry and the separation of penicillin from fermentation mixtures.

Leaching – This is the treatment of finely divided solids with a liquid.

Examples include oilseed extraction, extraction of sugar beets with hot water and extraction of medicinal compounds from plant roots, leaves and stems.

Humidification and dehumidification – Humidification refers to the increase of the vapor content of a gas stream by passing it over a liquid. Dehumidification on the other hand, involves the transfer of water vapor from the gas phase to the liquid phase. 

Membrane separation – This process involves the diffusion of a solute from one fluid stream through a semi-permeable membrane into another fluid stream. The components are selectively separated from the original solution from one side of the membrane to the other.

A membrane can be defined as a heterogeneous phase acting as a barrier to the flow of molecules and ionic species in liquid or vapor phases. If one component of the mixture travels faster in the membrane, a separation can be achieved. Based on their nature, heterogeneous barrier membranes can be classified into solid and liquid membranes.

Reverse osmosis and electrodialysis are examples of process that use membrane separation.

Crystallization – This is a process where a solid is formed from a liquid solution based on the difference in the solute concentration and its solubility at a certain temperature. In this process the solute transfer occurs from the liquid solution to a pure solid crystalline phase. When the concentration of the solute becomes higher than its solubility at a certain temperature, then the solute comes out of the solution is the form of a crystal.

Salt is extracted from sea water using crystallization.

Drying and Evaporation – Drying is the process of removing a small amount of water or other liquids from a solid material. The water is removed at a temperature below the boiling point of water by circulating air or another carrier gas over the material.  Evaporation is the removal of a large amount of water from solutions. The water is removed as a vapor at its boiling point.

In summary:

Separation Process	Separating Agent	Typical Applications
Adsorption	Adsorbent Solid	Separation of organics from gas.
Gas Absorption & Stripping	Solvent	Removal of CO2 from synthesis gas and CO2 and H2S from natural gas.
Distillation	Heat	Fractionation of crude oil.
Liquid-liquid Extraction	Solvent	Removal of aromatics from gasoline.
Solid-liquid Extraction	Solvent	Extraction of caffein from coffee.
Membrane separation	Membrane	Desalination of water.
Crystallization	Removal of heat	Production of salts and sugar.
Drying	Heat/Drying gas	Drying of fruits and polymer beads.