For a particular species, its concentration can be expressed in several ways.
In mass transfer applications, the only driving force
is the concentration gradient while other driving forces like temperature and
pressure gradients are kept constant. There needs to be a gradient of chemical
potential between two points to create a driving force that allows mass transfer
to occur.
A concentration gradient is a spatial
difference in the abundance of the chemical species.
A concentration profile is a sketch indicating
the magnitude of the concentration as a function of position and is often
superimposed on a process to indicate where these changes occur. It is
analogous to the velocity profile in fluid flow examples and illustrated below:
Mass concentration or molar concentration of components
and mass or mole fraction of species are used to express concentration gradients.
Mass Concentration
For any species i, the mass concentration is expressed
as ρi. It is defined as the mass of i per unit volume of a
multi-component mixture. This is expressed as follows and has the same units as
density:
Total mass concentration within a mixture is equal to overall density which can be expressed as follows, where n is the number of species in a mixture:
Mass Fraction
The mass fraction of species i (wi) is the
ratio of mass concentration of species i to the total mass density and can be
expressed as:
From the definitions used for mass concentration into the above
equation, we obtain the following expression:
Molar Concentration
The molar concentration (Ci) of component
is the number of moles of the ith component per unit volume of
mixture. The total concentration in the system can be obtained by adding up all
the molar concentrations of all the species in the mixture and is represented as:
To convert from mass to molar concentration, divide
the mass concentration of species i by its molar weight. For an ideal gas
mixture, the molar concentration of species i can be obtained from the ideal
gas law (PV = nRT) as follows:
Where:
- ρi is the partial pressure of species i in the mixture,
- T is the absolute temperature,
- R is the universal gas constant.
Thus, the total concentration in the gaseous system
can be represented by:
Mole Fraction
The mole fraction of species i in a mixture is found
by dividing the molar concentration of species i by total concentration in the
system and is expressed as;
and
The summation of mole fractions of species in a mixture always
adds up to 1 as shown:






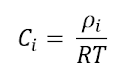
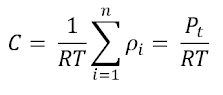







No comments:
Post a Comment