Mass Transfer is the net movement due to a concentration gradient of a component in a mixture from one location to another. Generally, this transfer occurs between two phases across an interface. Mass transfer can also be defined as the selective permeation through a non-porous polymeric material of a component of a gas mixture.
Mass transfer models can
be used to describe processes like the passage of a species through a gas to
the outer surface of a porous adsorbent particle and into the pores of the
adsorbent, where the species is adsorbed on the porous surface.
Mass transfer occurs through
two basic mechanisms:
(a) Molecular diffusion by random and spontaneous microscopic movement of individual molecules in a gas, liquid, or solid due to thermal motion
(b) Eddy (turbulent) diffusion by random macroscopic fluid motion.
Molecular Diffusion vs. Eddy Diffusion
Both diffusion types involve
different species moving in opposite directions. When a net flow occurs in one
of these directions, the total rate of mass transfer of the individual species
is increased or decreased by this bulk flow or convection effect, which is a
third mechanism of mass transfer.
Molecular diffusion is
extremely slow, while eddy diffusion, when it occurs, is orders of magnitude
more rapid.
Molecular diffusion
typically occurs in solids and fluid involving stagnant, laminar or turbulent
flow while eddy diffusion occurs in fluids with turbulent flow.
- In a binary mixture, molecular diffusion occurs due to one or more driving forces like:
- differences in concentration (ordinary diffusion)
- pressure (pressure diffusion). This requires a large pressure gradient which is achieved for gas mixtures with a centrifuge.
- temperature (thermal diffusion). Temperature gradients can be achieved by using thermal diffusion columns to separate liquid and gas mixtures
- external force fields (forced diffusion) that act unequally on the different chemical species present. This is achieved by using an electric field to cause ions of different charges to move in different directions at different speeds
When both molecular
diffusion and eddy diffusion occur, they take place in parallel and are
additive. Furthermore, they take place because of the same concentration gradient.
Describing diffusion
quantitatively
Assume that molecule A is diffusing between boundary 1 and 2 with fixed concentrations cA,1 and cA,2 respectively. The rate of diffusional mass transfer (moles/time) across an area, A, can be determined. A represents an area of y by z in the following illustration:
Fick’s Law of Diffusion
The concentration profile
is linear for any system with only pure diffusion (no convection, no reactions,
constant properties). Thus, Fick’s law can be approximated as:
The driving gradient for
diffusional mass transfer is the difference in concentrations i.e., cA,1 -
cA,2
|
Variable |
Definition |
Units |
|
ṄA,x |
moles
of species A transferred per unit time from location 1 to location 2 |
mol/s |
|
DAB |
the
diffusion coefficient of species A through medium B |
m2/s |
|
A |
the
area through which transfer occurs |
m2 |
|
cA,1 -
cA,2 |
the
concentration gradient between locations 2 and 1 |
mol/m3 |
|
x2-x1 |
The
distance between locations 2 and 1 |
m |
NOTE: the area for mass
transfer is not the ‘edge-view’ area but the ‘face-view’ area. This is the area
used in Fick’s Law and Fourier’s Law calculations:
In some cases, mass
transport occurs through a porous membrane with a pore fraction of εpore.
In such cases, the actual area available for mass transfer is only the porous
fraction of the total, and thus,
A = Aapparent εpore
Diffusion Coefficient
The diffusion coefficient,
DAB, is a proportionality constant between the molar flux due to
molecular diffusion and the gradient in the concentration of the species.
Theoretically, the
diffusion coefficient is proportional to the mean squared displacement divided
by the time elapsed:
The value of the diffusion
coefficient is determined through experiments, theory and estimation
The properties that
influence the diffusion coefficient of molecule A in solution B are:
- molecular weight of A and/or B,
- molecular size of A and/or B,
- molecular properties like charge, ionic strength, dipole moment of A and/or B,
- temperature,
- pressure.
Equimolecular counter diffusion
This occurs when the mass
transfer rates of the two components are equal and opposite.
It occurs in the case of
the box with a movable partition and also in a distillation column when the
molar latent heats of the two components are the same (λA = λB).


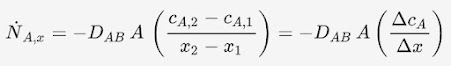







No comments:
Post a Comment