Process control can be defined the maintenance of a process output e.g., concentration, temperature or flow rate, within the desired specifications by continually adjusting other variables in that process.
Some examples of controlled processes include:
- Controlling the temperature of a stream of water by controlling the amount of steam added into the shell of a heat exchanger.
- Isothermally operating a jacketed reactor by controlling the mixture of cold water and steam that flows through the jacket of the reactor.
- Maintenance of a set ratio of reactants to be added to a reactor by controlling their flow rates.
- Controlling the height of fluid in a tank to make sure it does not overflow.
Control System Objectives
- Safety
- Economic Incentives
- Increasing efficiency
- Ensuring process stability
- Elimination of routine
- Protection of equipment
- Reduction of variability
Important definitions in Process Control
System: This is a combination of components that collectively
act and perform a certain objective.
Plant: This is the machine of which a particular
quantity or condition is to be controlled.
Process: This is the changing or refining of raw
materials that pass through or remain in a liquid, gaseous, or slurry state to
create end products.
Control: in process industries, this refers to the
regulation of all aspects of the process. Precise control of temperature,
pressure, pH, level, oxygen, foam, nutrient, and flow is important in numerous
process applications.
Sensor: This is a measuring instrument that detect the
vale of the measurable variable as a function of time. The most common
measurements are of flow (F), temperature (T), pressure (P), level (L), pH and
composition (A, for analyzer).
Set point: This is the value at which the controlled
parameter is to be maintained.
Controller: This is a device that receives a
measurement of the process variable, compares it with a set point representing the
desired control point, and adjusts its output to minimize the error between the
measurement and the set point.
Error Signal: The signal resulting from the difference
between the set point reference signal and the process variable feedback signal
in a controller.
Feedback Control: A type of control where the
controller receives a feedback signal representing the condition of the
controlled process variable, then compares it to the set point and adjusts the
controller output accordingly.
Steady-State: This is the condition when all of the process
properties are constant with time, transient responses having died out.
Transmitter: This is a device that converts a process
measurement (pressure, flow, level, temperature, etc.) into an electrical or
pneumatic signal that is suitable for use by an indicating or control system.
Controlled variable: This is the process output that
is to be maintained at a desired value by adjustment of a process input.
Manipulated variable: This is the process input that
is to be adjusted to maintain the controlled output at set point.
Disturbance: This is a process input (other than the
manipulated parameter) which affects the controlled parameter.
Process Time Constant (τ): This is an amount of time
counted from the moment the variable starts to respond that it takes the
process variable to reach 63.2% of its total change.
Block diagram: This is the relationship between the input and the output of
the system. This is commonly illustrated as a figure. Examples are shown in the diagram below:
Transfer Function: This is the ratio of the Laplace
transform of the output (response function) to the Laplace transform of the input (driving
force) under the assumption that all the initial conditions are zero unless given
another value.
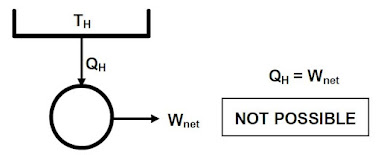
Closed-loop control system: is a mechanical or electronic device that
automatically regulates a system to maintain a desired state or set point
without any human interaction. It uses a feedback system or sensor.
Advantage: more accurate than the open-loop control
system.
Disadvantages:
(1) Complex and expensive
(2) The stability is the major problem in closed-loop
control system
Open-loop control system: In this system there is no feedback to the controller about the
current state of the system. There is no self-regulating mechanism and human
interaction is typically required.
Advantages:
(1) Simple construction and ease of maintenance.
(2) Less expensive than closed-loop control system.
(3) There is no stability problem.
Disadvantages:
(1) Disturbance and change in calibration cause
errors; and output may be different from what is desired.
(2) To maintain the required quality in the output,
recalibration is necessary from time to time



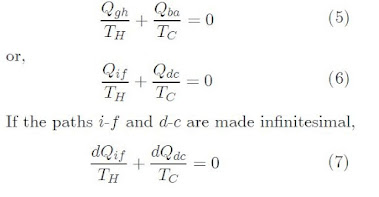






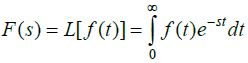
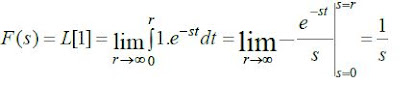













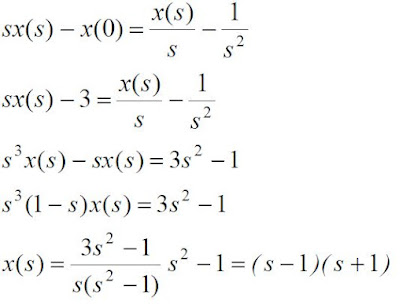

.png)




