Let us consider a closed system that undergoes a reversible process from an initial state, i, to a final state, f, using a process path. It is possible to draw an adiabatic and isothermal path from the initial and final state as shown:
The work done by the system going from the state i to f is the area under the process path on a P − V diagram. Between two adiabatic lines, it is possible to find an isothermal path gh such that the area under the curve ighf is equal to the actual work. This can be calculated as follows:
The above statements lead us to the theorem of Clausius which states:
Given
any reversible process where the temperature changes in any prescribed manner,
it is possible to find a reversible zigzag process that consists of adiabatic-isothermal-adiabatic
steps such that the heat interaction in the isothermal step equals the heat
interaction in the original process.
Let us consider a system that undergoes a reversible and cyclic process with any two points, i and f, on a process path. The adiabatic lines that pass through these points intersect the cycle path at points c and d. Using the theorem of Clausius, it is possible to represent the paths i - f and d - c by adiabatic-isothermal-adiabatic paths as i - g - h - f and d - b - a - c, respectively in the following graph. Also note that Qif = Qgh and Qdc = Qba
If
we take the heat interaction of the path i – f, to be from
a reservoir at TH and in path d – c from a reservoir
at TC, we see that the cycle i-g-h-d-b-a-i is nothing but a
Carnot cycle. Thus, using equation 21 from this blog entry, we can write:
An infinite number of infinitesimal cycles, beginning at j and ending at k, cover the entire cycle, we then obtain:
To evaluate ΔS for an irreversible process, we can devise a reversible path(s) between the same initial and final states and then evaluate dQrev/T over this reversible path
For an adiabatic and reversible process dQrev = 0 thus equation 11 simplifies as:
ΔS = 0 (12)
A
process where the entropy remains constant is called an isentropic
process.



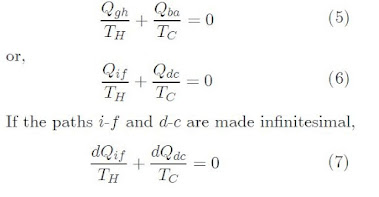





No comments:
Post a Comment