Laplace transformations are a mathematical technique used to solve differential equations. Numerous mathematical problems are solved using transformations. The idea is to transform a difficult problem into another form that is easier to solve. Once the problem is solved, the inverse transform can be used to solve the original problem.
The Laplace Transformation of a function f(t) can be converted into a function f(s) using the following equation:
Example 1: Find the Laplace Transform of f(t) = 1
Solution:
Example 2: Find the Laplace Transform of f(t) = eat
Solution:
Example 3: Find the Laplace Transform of f(t) = sin (wt) and f(t) = cos (wt)
Solution:
Example 4: Find the Laplace Transform of f(t) = cosh (wt) and f(t) = sinh (wt)
Solution:
Below is a summary table for common Laplace Transformations
Shifting Theorem
The common expression is as follows:
Example 5: Find the Laplace Transform of f(t) = eat cos (bt)
Solution:
Example 6: Find the Laplace Transform of f(t) = sin (3t).e5t
Laplace Transforms for Derivatives
The following are the general equations for different ordered differential equations:
Example: Find the Laplace Transform of the function x(t) which satisfy the following differential equation and initial condition:
Solution:
Take the Laplace transform of both sides of the equation.
Laplace Transforms for Integrals
The general equation for Laplace transforms of integrals is as follows:
Example: Find x(s) for the following equations
Solution
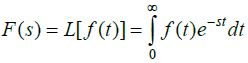
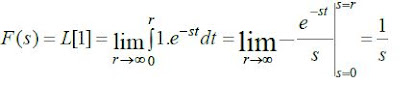
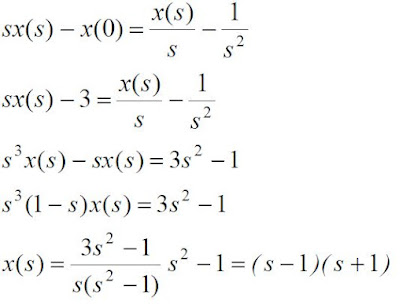
please also make an entry for inverse laplace, would be helpful
ReplyDelete